Character Tables for Point Groups used in Chemistry
Character Tables are an important tool derived from Group Theory and are used in many parts of molecular chemistry, particularly in spectroscopy. On this page, you can find character tables for all remotely interesting discrete axial point groups, plus the groups for cubic and icosahedral symmetry.
- Some point groups have irreducible representations with complex characters. These have been eliminated by creating reducible representations with real-valued characters, as is common in chemistry (applies to point groups Cn, Cnh, S2n, T, Th).
- All point groups up to 128-fold rotations are included. This is far more than anyone is likely ever to need. To access the character tables, use the list below or enter the name of the point group into the search field (needs JavaScript).
- Symmetry-adapted linear combinations of Rotations and Cartesian products up to sixth order (i functions) are listed. This is not fully implemented for icosahedral symmetry, though.
- Tables for the symmetry of multipoles, the direct multiplication of irreducible representations and the correlations to lower symmetry groups are provided. These are calculated inside your browser, so they might not be available on some old browsers.
- Moreover, some interactive features are available to those who have reasonably standard-obeying browsers.
- A form for decomposing reducible representations into irreducible ones, with particular emphasis on the common case of vibrational analysis.
- A form for direct products involving an arbitrary number of factors
- The multipole symmetry analysis can be extended up to arbitrary order, and (for axial groups) a detailled analysis of the different m values can be requested.
- Examples (both geometrical object and molecules) are gives for every point group if possible.
Output Explained
The output is shown as a number of tables that usually behave intelligently on hovering; it is often possible to click elements on the edges of the table to highlight rows, columns or other elements permanently. Saving a page (together with styles and scripts, which are the same two files for all tables) creates a fully functional offline copy.
Most output should be self-explaining. However, in the “Notes” section, several issues are mentioned that merit an explanation.
- The order of the group is the number of symmetry operations in the group.
- The order of a symmetry operation is the minimum exponent converting that symmetry operation into the unit operation (or, alternately: All symmetry operations are roots of unity of some order). The principal axis is the symmetry element giving rise to the symmetry operation with the highest order.
- Some groups may be known by different names, although most of the alternate names will rarely occur in the more recent literature.
- The generators are those symmetry elements that generate, by successive multiplication, all symmetry operations of a group. For groups with more than one generator, the choice of generators becomes to some degree arbitrary; the character table as printed here reflects a particular, canonical choice. All point groups are genrated by two elements, with the exception of Cn and Sn (includes C(2n+1)h), which have only one, and D2nh, which have three. For some odd-numbered groups (Cnh, Dnh and Dnd), the canonical choice employs redundant generators.
- Groups are isomorphic if their multiplication tables are identical up to permutation and labelling. The same will hold for the character tables of isomorphic groups.
- The order of the lowest (permanent) multipole moment of a group is the order of the lowest spherical harmonic that transforms trivially. It is 2 or 4 for axial groups, 8 or 16 for cubic groups and 64 for icosahedral groups. Groups that allow a permanent dipole moment are called “polar point groups”, and they can be defined by demanding that some points other than the origin must stay fixed under all symmetry operations (Cn, Cnv and the special cases C1h≡Cs, D1=C2, D1h=C2v).
- Abelian groups with a order of the principal axis greater than two have complex-charactered irreducible representations that are conventionally converted into real-charactered degenerate reducible representations (this also applies to T and Th, but to no other cubic group). This has to be borne in mind because it neccessitates a small modification in the projection formula to “reduce” reducible representations into irreducible ones.
- Some groups will display special properties which are often due to arithmetic peculiarities of the cosine function triggered by the order of the principal axis.
- In particular, some have integer characters which makes them compatible to periodic lattice symmetry. These are called “3D crystallographic point groups”, because they (and only they) satisfy the crystallographic restriction theorem in three dimensions.
- However, every point group is crystallographic in a sufficiently high-dimensional space: n−1 dimensions are always enough, but only prime numbers go to this limit; for even n, the upper limit is n/2−1 dimensions, and for compound odd n, it is n−3. Excepting isometric groups, only even numbers of dimensions have to be considered, because if a linear group is crystallographic in 2k+1 dimensions, then it is also crystallographic in 2k dimensions.
- Unrelated to this, some point groups have characters representable by integer numbers and (possibly nested) square roots; the corresponding polygons are then constructible in the classical sense (compass and ruler). All 3D or 4D crystallographic point groups are constructible, but the converse is not true, and the statement does not generalize to higher dimensions.
- Groups that are not constructible additionally need complex numbers and odd roots to write algebraic expressions for the characters. Those which need only square and third roots are constructible by any method that allows angle trisection, like origami and neusis construction.
- Groups containing an C4 or S4 symmetry operation will have at least one direct product of E representations that decomposes into a direct sum of four nondegenerate irreducible representations. For the same reason, these groups show a complication in lowering of symmetry: Symmetry alone does not in all cases determine the subsymmetry reached by following a particular degenerated normal mode.
- Some non-Abelian point group have distinct classes of symmetry operations of the same type, e. g. σv vs. σd. Usage of character tables presupposes that the user follows some conventions; these conventions (“standard orientation”) are described in detail for all these groups (C2nv, D2n, D2nh, D2nd).
The interactive features, in particular processing of form input, should also work without much explanation. Note the that form for the Reduction Formula accepts not only character values, but also directly the number of atoms stationary under the symmetry operation; just enter #n for n unmoved atoms. See below for more details on this.
Molecular Examples
I have tried hard to find real molecules exemplifying the point groups (full support for n≤6, partial 7≤n≤10). While I was not successful for all point groups, I could find a lot more examples than I originally expected, for example, the “molecular wheels” with D10h symmetry.
While some of the example molecules have been characterized by X-ray crystallography, some others are known only from theoretical studies, and some are just educated guesses on my part. Keep in mind that non-crystallograhic symmetries (with symmetry axes of order five, seven, eight, …) can never be confirmed by crystallography, and that small deviations from the idealized symmetry are common in crystals. Also, systems with internal rotations or other “floppy” degrees of freedom do not have a rigid structure, and assigning a point group to them involves some idealization.
The examples stem chiefly from inorganic (including coordination commpounds and clusters), metallorganic and organic chemistry; supermolecular chemistry and biochemistry have been mostly avoided.
Browser Compatibility
Sad to say, but browser compatibility is still an issue in the middle of the second decade of the 21st century.
The main, or rather only, culprit here is Microsoft. If you buy ($$$) a kind of operating system that comes with some version of Internet Explorer, then that browser has a fixed number of capabilities and bugs which behave totally invariant with respect to time, this is, they will persist unaltered till Judgement Day. Updates to later versions need extra work by the user, and are generally unavailable for some combinations of system parameters. Compare, if you download (free!) Firefox, Chrome, Opera or whatever you want, this will usually update itself automatically every few weeks, fixing existing bugs and teaching the browser more tricks that web authors can rely upon as “generally available”.
Now, it does not help that Microsofts rendering engine is also (a) the most buggy, (b) most idiosyncratic and (c) least capable, not to mention that (d) it is not available for testing to web authors who develop their pages on other operating systems than The-One-Which-Cannot-Be-Named.
So, while I can be reasonably sure that these Character Tables perform well with Browsers based on Gecko (Firefox, Seamonkey), WebKit (Chrome, Safari) and Opera’s old proprietary Presto engine, I simply have no idea whether they work well on Internet Explorer (no, I will not install a gigabyte-heavy virtual machine that expires every few months). Having performed painful wine workarounds, I do know, however, that Internet Explorer 7 and lower fail disastrously because they cannot recognize linebreaks, and that Internet Explorer 8 knows linebreaks but fails on something else long before the job is done.
Technical Notes
The Character Tables you (hopefully) see on your screen are mostly produced inside your browser. The server serves a crude text file with superficial HTMLification that can be used as a fallback. A long sequence of JavaScripts takes this file as input, creates an internal representation of the character table and associated information, calculates loads of derived data and then overwrites its input with the much more advanced tables you are likely to see here.
This proved the most convenient solution because I cannot run server-side scripts and do not want to upload scores of HTML files whenever a fix to the algorithm is made. Moreover, it has the additional benefit that the stuff also works offline. However, it does put some pressure on the visitor, whose hardware has to perform a lot of calculations in addition to all the rendering work (which is not trivial in itself, and the interactivity involves tons of event handlers and CSS transitions). This should not be much of a problem for PC users, as even my small laptop can calculate and render the tables for small and medium-sized groups is a few seconds. The situation might be difficult for smartphone users, but the I don’t see too much sense in trying to read extended tables on a display 7 cm large.
I do provide some rudimentary fallbacks for browsers that don’t understand CSS gradients and box shadows, but input form validation is assumed to work with the CSS3 pseudo-classes. On machines that do not support those, users are responsible for what they type, as they will not get much feedback in case of errorneous input.
Notational Conventions
Character tables found in various sources will usually agree on the naming of symmetry operations and irreducible representations, although they might list them in different orders. The sorting order shown in my tables is something I consider rational, but some readers might have different expectations. Give particular care to the arrangement of Snk operations in groups Cnh and Dnh for even n.
In the literature, noninteger characters are handled in various ways and typically represented as cosine values or by use of the complex exponential function. I consider it more convenient to show them numerically and give the exact representation in an appendix. This is really the only option for the involved radical expressions as offered for some higher groups in addition to the cosine representation.
Irrational characters exist only in E races (and T races of icosahedral groups), and are always of the form 2*cos(2πk/n) (n being the order of the principal axis and k ≤ n/2). For n even, this means that any character value may appear with positive or negative sign, but for some odd groups (Cn, Cnv, Dn), there will be separate sets of positive and negative character values. This is reflected in the glosses: In the even cases, only positive numbers are listed, in the odd cases all numbers as they appear.
With respect to Cartesian products, authors are divided whether to show expressions relating to improper lower angular momenta in the tables. For example, one of the six possible Cartesian products of order two transforms as a scalar (x2+y2 for axial and x2+y2+z2 for isometric groups); it is doubtful whether such an entry is helpful in a character table, and I do not show it there.
Most sources follow the typographical convention that the subscript letters v,h,d in the names of point groups are printed in italics; I consider that ill-chosen, as italics are reserved for variables. The difference becomes clear when expressions like C2n and C2v are compared.
Cartesian Products
The Cartesian products are trivariate polynomials (in x, y and z) adapted for a particular symmetry. If written as a simple sum, all terms have the same order ℓ (the angular momentum quantum number of the corresponding spherical harmonic). For example, xy(x2−y2) equals x3y−xy3 and is of order ℓ=4 (it is a g function, actually g4−g-4).
Starting with order two, some Cartesian products have the symmetry of lower angular momenta. For example, x2+y2+z2 is of order two (apparently a d function), but transforms as order zero (s function). Similarly, xz2+yz2+z3 looks like an f function, but transforms as a p function. I have decided to exclude these “improper” Cartesian products from my character tables, although some literature actually shows them.
There are several possible choices for symmetry adapted Cartesian products. A natural choice would be atomic hydrogen orbitals (2p, 3d, 4f etc), which are directly derived from spherical harmonics (actually, these are the essentially the “regular solid harmonics”, a subset of the hydrogen functions where ℓ=n−1). This has the big advantage that not only the “improper” Cartesian products are naturally excluded, but also the resulting terms are orthogonal to each other and to the “improper” ones (they are in an orthogonal subspace). However, it also has disadvantages, and so I have decided against it.
-
In axial symmetries, some of the hydrogen atomic orbitals are more complicated than necessitated by the symmetry (for example, z2 is sufficient, but the atomic orbital is 2z2−x2−y2). This occurs whenever |m|+1<ℓ and thus becomes really an issue for higher angular momenta.
Thus, I have decided to use simpler expressions that derive from the full atomic orbitals by ignoring all powers in z except the highest and cutting all terms x2+y2. This is a substantial simplification; for example, the function g2+g-2, in full (6z2−x2−y2)(x2−y2), is represented as z2(x2−y2); another example is i2−i-2, in full xy(33z4−17z2+x2+y2) and in the abbreviated convention xyz4.
It is common to refer to atomic hydrogen orbitals by such “nicknames”; however, in the literature, such abbreviations are sometimes pushed further than axial symmetry allows: For example, the function g3+g-3 is sometimes nicknamed zy3; the correct term is yz(3x2−y2), and this cannot be further simplified without losing essential symmetry properties. In my tables, I give the simplest form that adheres strictly to axial symmetry.
This choice has consequences for the orthogonality relations: Functions for the same value of m are no longer guaranteed to be orthogonal (even and odd functions, of course, are always in orthogonal subspaces). Moreover, the orthogonality to the “improper” products is lost (there is a kind of “lower angular momentum contamination”).
For those point groups that have a principal axis of order one or two, the terms could be radically simplified, as any simple product is already symmetry-adapted. For consistency and easy correspondence to atomic orbitals, the products are nevertheless given in standard form. In the same vein, no simplification is employed in the case of degenerate pairs: For example, the f3±f-3 functions, correctly x(x2−3y2) and y(3x2−y2), could be simplified to x2y and xy2 whenever they are degenerate (i.e., in all point groups where the order of the principal axis is larger than two but does not divide six: 4,5,7,8,…).
-
For cubic point groups, Cartesian products derived from spherical harmonics form a cumbersome base if ℓ>2, this is, f functions and higher. Therefore, I have built symmetry-adapted linear combinations of primitive products (xryszt) from scratch, trying to keep them as simple as possible. By construction, they have no relation to spherical harmonics (and thus, angular momentum).
There are still some arbitrary choices in these products. These could have been reduced (but not eliminated completely) by forcing the products to be orthogonal to the “improper” ones, but this is hardly worth the trouble. For example, instead of xyz2, the orthogonality constraint would have yielded xy(2z2−x2−y2).
-
I have not yet succeeded in deriving symmetry-adapted Cartesian products for icosahedral point groups, and I consider this a pretty irrational task.
Note that i functions (ℓ=6) are a natural limit for Cartesian products. For higher angular momenta, symmetry-adapted Cartesian products do exist, but not all of them factorize inside the real numbers. This is related to the fact that many cosines cos(2π/m) (m≥7) cannot be calculated from integers by the operations of addition, subtraction, multiplication, division and real square root extraction. While the terms for cos(2π/7), cos(2π/9), cos(2π/13) and cos(2π/14) are comparatively manageable (complex expressions involving square and third roots), the one for cos(2π/11) is madly complicated, spanning many lines of text full of complex numbers, square and fifth roots.
For the chemistry student, the most typical use of character tables is the vibrational analysis of molecules. This leads to a reducible representation in the molecule’s point group that must be reduced, i.e., projected onto the irreducible representations by using a scalar product looping over the symmetry operations. The result is a direct sum (basically a linear combination) of irreducible representations. Since you read this character table with a computer, it seems a reasonable idea to use that device also for doing the actual computation.
The reduction form on each character table page expects characters for all symmetry classes, performs the projection and reports all nonzero coefficients. As input, either the characters or a hash mark (#) followed by the number of stationary atoms is accepted; the latter gets multiplied with the character of the Cartesian representation to yield the character used in the projection. Ill-formed input is indicated by the input box turning red. Calculation starts as soon as all input boxes contain valid input.
The projection must yield integer coefficients; if the result is noninteger, then an error message is produced (the most likely reason being wrong user input). In case of point groups containing noninteger characters, a roundoff threshold has been chosen that will usually be satisfied if all input characters are accurate to at least three digits right of the decimal point. In case of a “near miss”, it might be useful to relax the threshold to a value greater that the number reported in the error message, although this increases the risk that erroneous input might be accidentially accepted. Setting the threshold to one will accept any random input and produce meaningless output therefrom. Results that do not even have the right dimensionality are suppressed, but this simple check cannot catch every input error.
A simpler form allows to reduce arbitrary n-ary direct products of irreducible representations into direct sums. This is conceptually simpler, because a projection failure cannot occur.
The implementation of the algorithm is solid in principle but rather ad-hocish in the details; always watch out for Bugs in Dark Corners. This said, the calculation seems to work reliably with Firefox, Chrome, Safari 4 and Opera 12 (also Opera 25). Those browsers which do not support HTML5 will fail on input validation, which is not a problem if the input is correct. The whole thing works only rudimentarily with Internet Explorer 8 and 9, and the output of these browsers is aesthetically crippled. Other browsers have not been tested. Because the code is implemented in JavaScript and takes all necessary information from the document itself, the forms should remain functional if you download and save the full page (including styles and scripts).
For those interested in the nasty details, I mention that Internet Explorer 8 and 9 fail on innerHTML operations inside tables, do not support the the HTML5 style input validation using regular expressions in the pattern attribute triggering an :invalid pseudo-attribute, and have a tendency to mess up every table layout. onChange events are not fired when I expect them, but only after focus is shifted from the INPUT element, and onKeyPress appears to be dysfunctional. Also, storing some information as private attributes inside the DOM does not really work, as these attributes turn out to be write-only.
Multiplication Table
A conventional multiplication table for binary products of irreducible is also offered. That table is calculated on the fly in your browser, which may take significant time (fourth order in the number of classes) for really large groups.
This table makes a distinction between symmetric and antisymmetric products for the multiplication of a degenerate irreducible representation by itself. In the context of orbitals and electronic states, the antisymmetric product corresponds to triplet states (antisymmetric spatial part of the wavefunction) and the symmetric to singlet states; in the context of vibrational combination bands, the antisymmetric product corresponds to nothing as vibrational wavefuntions must be symmetric.
The direct product of an irreducible representation j with another one k can be written as
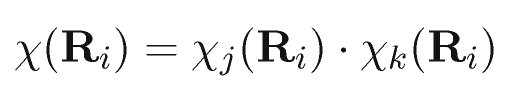 where the χ(Ri) is the character of the symmetry operation Ri in the product representation. If the product is between a degenerate irreducible representation and itself (j=k), then the product can be split into a symmetric and an asymmetric part
where the χ(Ri) is the character of the symmetry operation Ri in the product representation. If the product is between a degenerate irreducible representation and itself (j=k), then the product can be split into a symmetric and an asymmetric part
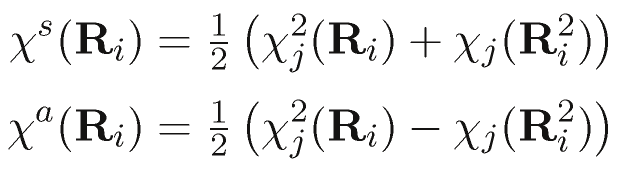 where Ri2 is the square of Ri (and therefore, in the general case, a distinct symmetry operation). With the additional information which symmetry operation is the square of a given symmetry operation, the antisymmetric product becomes available from the character table. However, this is almost moot as in all axial groups the antisymmetric product of an E with itself is always A2 (drop the 2 if it does not apply, and add a prime or a g if necessary), and it is only in the isometric groups that this result becomes interesting.
where Ri2 is the square of Ri (and therefore, in the general case, a distinct symmetry operation). With the additional information which symmetry operation is the square of a given symmetry operation, the antisymmetric product becomes available from the character table. However, this is almost moot as in all axial groups the antisymmetric product of an E with itself is always A2 (drop the 2 if it does not apply, and add a prime or a g if necessary), and it is only in the isometric groups that this result becomes interesting.
Subgroups
The analysis of subgroups is pretty challenging, because character tables (or at least parts thereof) are needed for all subgroups to determine the correlation of irreducible representations. Also, the question of standard orientation (which can usually be ignored) becomes rampant, especially in the cubic groups. Finally, that task may become a benchmark for your browser, because significant amounts of data are produced during the computation and have to be stored in voluminous data structures, not to speak of the rendereng of the large table produced.
By intention, the module will automatically produce all subgroups (both in standard orientation and in most non-standard orientation) for axial point groups; subgroups are counted as “distinct” if they draw their symmetry operations from different classes of the parent group. For cubic and icosahedral point groups, a hand-selected list consisting of all standard-oriented and off-standard-oriented point groups is evaluated. Characters (and thus, irreducible representations) in the reduced symmetry are evaluated by a lazy algorithms that uses just the generator elements (plus a few kludges). From this, a complete correlation table is produced.
A related feature is the determination of subgroups reached by distortion along symmetry-adapted coordinates (e. g., normal coordinates). While this is well-defined for Abelian groups (including those with complex irreducible representations that are conventionally combined into “pseudo-degenerates”), it may run into ambinguity for some truly degenerate irreps. The results are displayed in the first column of the correlation table.
- An entry like → 2 C3h means that both components of an E representation distort into equivalent C3h groups, i. e., the symmetry operations of the daughter groups are paiwaise equivalent under the parent group’s class structure. This is the behaviour of all Abelian groups, for example C9h.
- If the two E components lower the symmetry to different subgroups, then this is written as → D3 C3v. The two subsymmetries are either isomorphic, or one contains the other (example: D9h).
- As a special case, → D3 D3 indicates that the two components of the E distort into inequivalent subsymmetries of the same type, i. e., the symmetry operations of the D3 daughter groups come from different classes of the parent group (example: D18).
- The notation → [ 2 D3 ] marks the case that the parent group contains two distinct D3 subgroups, and both components of the E distort into the same type of D3, yet the symmetry race of the coordinate alone does not decide into which (example: D12). This behaviour is linked to the presence of 4n-fold axes.
- An even more confusing case can arise in D2nd groups, due to the presence of S4n: A given E might lower the symmetry into one of two possible subsymmetries, which are always isomorphic. This is written as → [ 2 D3 | 2 C3v ] and implies that the resulting subsymmetry is either D3 for both components, or C3v for both components of the E (example: D6d).
Hovering over the subgroup symbols in the first column will highlight the entries for the respective subgroup in the same row. Note that the distortion analysis is not implemented for the icosahedral groups.
Download
The complete set of all character tables up to n=128 (in plain text format) can be downloaded as an XZ-compressed tar file. If you need other point groups, drop me a note.
Note that this is just a sparetime and fun project. There might be bugs of any magnitude; no warranty whatsoever is offered. If you find a mistake, please let me know so that I can correct it.
Algorithm to Generate Character Tables
The character tables shown here were generated by a short Fortran program. Generation is done in steps, coarsely outlined by the following algorithm.
- For Cn, generate a character table with a trivial A representation, an alternating B representation if n is even, and an appropriate number of E representations. The E1 has characters equal to the double cosine of the respective rotation, 2cosφ, the E2 has 2cos2φ etc.
- For Cnv and n even, generate Cn, add each a new class for σv and σd, and double the rows for A and B (with positive or negative characters for the new classes); for n odd, add one σv class and double the A representation. E representations take a zero character for the new classes.
- For Cnh and n odd, generate Cn. Then, generate new classes by multiplying the existing ones with σh, and double all irreducible representations, taking existing characters for the new classes and multiplying them by 1 or −1.
- For Cnh and n even, do the same but use i as the generator. This procedure yields the new symmetry operations in an unintuitive order (related to the difference between mirror-reflexion and roto-inversion axes). The character tables shown on these pages have these entries resorted, which is not always done in the literature.
- S2n is identical to C2n except the labelling of the classes. However, this is the conventional approach for S4n only; for S4n+2, the character table is built from C2n+1 by adding a center of inversion similar to C2nh.
- For Dn, generate Cn. Then, add C2 rotations similar to the Cnv case.
- For Dnh, generate Dn. Then, proceed as in Cnh.
- For Dnd and odd n, generate Dn, then double the table by adding an additional center of inversion (as in Cnh).
- For Dnd and even n, the conventional form of the character table is arrived at by starting with S2n, then adding one C2′ and one σd class, similar to Cnv. This special treatment is necessary because while D2n has distinct C2′ and C2″ classes, these collapse into one single C2′ in the D2nd group.
- Similar procedures can be used to build Td, Th and O from T, Oh from O and Ih from I.
Labelling and sorting needs some care, because conventions differ for different point groups.
The transformation of rotations and Cartesian products can be arrived at easily for Cn and S2n: Both components of a ±m pair (e.g., d±2 aka x2−y2 and xy) will always belong to the same symmetry race; moreover, the characters for the combined representation of one ±m pair are just 2cos|m|φ (add a sign (−1)ℓ−|m| for S2n, where ℓ is the order of the product or the angular momentum quantum number of the corresponding spherical harmonics). For m=0, the same formula applies without the prefactor 2; since cos(0)=1, this component always transforms trivially in Cn, while in S2n this is true only if ℓ is even.
When the groups are subsequently augmented with additional symmetry operations, I chose to keep track of the various steps of irrep doublings, and move the basis functions to the positive or negative offspring row, depending on the behaviour of that basis function under the newly introduced symmetry element (I used a big table for that). This approach might appear unelegant, but has the advantage that neither complex arithmetics nor case distictions between one- and two-dimensional symmetry races are needed.
Real Radicals
All irrational character values have the form 2*cos(2*m*π/n), where n is the order of the principal axis and m<n. For some point groups (n=3,4,5,6,8,10,12,15,16,17,20,24,30,32,34,40,48,51,60,64,68,80,85,96,102,120,128,136,160,170,192,204,240,255,256,257,…), this can also be written with real radicals.
I have managed to derive algebraic expressions for almost all cases where this is possible (starting with n=85, some cosines are still missing). Possibly, some of the expressions given could be further simplified, but I am not motivated. For your pleasure, here is the full list in a format most programming languages (or bc) can directly understand. They can also be displayed in conventional form with graphic square roots if your browser allows (don’t expect typographic excellence, it’s HTML and not TEX).
0.01227153828571992608 = cos(127*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.01636173162648678164 = cos(95*pi/192) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(3))))))/2
0.02454122852291228803 = cos(63*pi/128) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2))))))/2
0.03079505855617035387 = cos(25*pi/51) = (-1-sqrt(17)-sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/16
0.03271908282177614206 = cos(47*pi/96) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(3)))))/2
0.03680722294135883232 = cos(125*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.03925981575906860902 = cos(39*pi/80) = sqrt(4-sqrt(8+sqrt(2)+sqrt(10)+2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.04618345864573959195 = cos(33*pi/68) = sqrt(8-sqrt(2)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17)))))/4
0.04906767432741801425 = cos(31*pi/64) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))/2
0.05233595624294383272 = cos(29*pi/60) = (sqrt(10)-sqrt(2)-sqrt(6)+sqrt(30)+2*(1-sqrt(3))*(sqrt(5+sqrt(5))))/16
0.06132073630220857778 = cos(123*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.06540312923014306682 = cos(23*pi/48) = sqrt(2-sqrt(2+sqrt(2+sqrt(3))))/2
0.07356456359966742353 = cos(61*pi/128) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2))))))/2
0.07845909572784494503 = cos(19*pi/40) = sqrt(8-sqrt(2)-sqrt(10)-2*sqrt(5-sqrt(5)))/4
0.08172107413366822375 = cos(91*pi/192) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(3))))))/2
0.08579731234443989046 = cos(121*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.09226835946330199524 = cos(8*pi/17) = (-1+sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16
0.09801714032956060199 = cos(15*pi/32) = sqrt(2-sqrt(2+sqrt(2+sqrt(2))))/2
0.10452846326765347140 = cos(7*pi/15) = (sqrt(30-6*sqrt(5))-sqrt(5)-1)/8
0.11022220729388305881 = cos(119*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.11428696496684639812 = cos(89*pi/192) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(3))))))/2
0.11753739745783764411 = cos(37*pi/80) = sqrt(4-sqrt(8-sqrt(2)+sqrt(10)+2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.12241067519921619850 = cos(59*pi/128) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2))))))/2
0.13052619222005159155 = cos(11*pi/24) = sqrt(2-sqrt(2+sqrt(3)))/2
0.13458070850712618632 = cos(117*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.13815635495188219823 = cos(31*pi/68) = sqrt(8-sqrt(2)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17)))))/4
0.14673047445536175166 = cos(29*pi/64) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))/2
0.15339165487868537265 = cos(23*pi/51) = (-1+sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/32 - sqrt(6)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/16
0.15643446504023086901 = cos(9*pi/20) = (sqrt(2)+sqrt(10)-2*(sqrt(5-sqrt(5))))/8
0.15885814333386144168 = cos(115*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.16289547339458873948 = cos(43*pi/96) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(3)))))/2
0.17096188876030122636 = cos(57*pi/128) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2))))))/2
0.17901686127663268204 = cos(85*pi/192) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(3))))))/2
0.18303988795514095852 = cos(113*pi/256) = sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.18374951781657033157 = cos(15*pi/34) = sqrt(2)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/8
0.19509032201612826785 = cos(7*pi/16) = sqrt(2-sqrt(2+sqrt(2)))/2
0.20711137619221854971 = cos(111*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.20791169081775933710 = cos(13*pi/30) = (sqrt(3)-sqrt(15)+sqrt(10+2*sqrt(5)))/8
0.21111155235896516592 = cos(83*pi/192) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(3))))))/2
0.21393308320649743991 = cos(22*pi/51) = (1-sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/32 + sqrt(6)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16
0.21910124015686979723 = cos(55*pi/128) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2))))))/2
0.22707626303437320759 = cos(41*pi/96) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(3)))))/2
0.22895054995013407691 = cos(29*pi/68) = sqrt(8-sqrt(2)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17)))))/4
0.23105810828067111964 = cos(109*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.23344536385590541177 = cos(17*pi/40) = sqrt(8+sqrt(2)-sqrt(10)-2*sqrt(5+sqrt(5)))/4
0.24298017990326388995 = cos(27*pi/64) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))/2
0.25486565960451457155 = cos(107*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.25881904510252076235 = cos(5*pi/12) = sqrt(2-sqrt(3))/2
0.26671275747489838633 = cos(53*pi/128) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2))))))/2
0.27144044986507425334 = cos(33*pi/80) = sqrt(4-sqrt(8+sqrt(2)-sqrt(10)+2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.27366299007208286354 = cos(7*pi/17) = (1+sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/16
0.27458861818493234148 = cos(79*pi/192) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(3))))))/2
0.27851968938505310521 = cos(105*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.29028467725446236764 = cos(13*pi/32) = sqrt(2-sqrt(2+sqrt(2-sqrt(2))))/2
0.30200594931922806700 = cos(103*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.30590302009655346276 = cos(77*pi/192) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(3))))))/2
0.30901699437494742410 = cos(2*pi/5) = (sqrt(5)-1)/4
0.31368174039889147666 = cos(51*pi/128) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2))))))/2
0.31779141958190162617 = cos(27*pi/68) = sqrt(8-sqrt(2)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17)))))/4
0.32143946530316158070 = cos(19*pi/48) = sqrt(2-sqrt(2+sqrt(2-sqrt(3))))/2
0.32531029216226293414 = cos(101*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.33235479947965966456 = cos(20*pi/51) = (1-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/32 - sqrt(6)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16
0.33688985339222005069 = cos(25*pi/64) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))/2
0.34611705707749297647 = cos(31*pi/80) = sqrt(4-sqrt(8+sqrt(2)+sqrt(10)-2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.34841868024943456842 = cos(99*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.35225004792123350653 = cos(37*pi/96) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(3)))))/2
0.35836794954530027348 = cos(23*pi/60) = (sqrt(2)-sqrt(6)+sqrt(10)-sqrt(30)+2*(1+sqrt(3))*(sqrt(5-sqrt(5))))/16
0.35989503653498814878 = cos(49*pi/128) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2))))))/2
0.36124166618715294874 = cos(13*pi/34) = sqrt(2)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/8
0.36751593659470356541 = cos(73*pi/192) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(3))))))/2
0.37131719395183754341 = cos(97*pi/256) = sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.38268343236508977173 = cos(3*pi/8) = sqrt(2-sqrt(2))/2
0.38978587329267936908 = cos(19*pi/51) = (-1-sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/16
0.39399204006104810860 = cos(95*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.39774847452701105205 = cos(71*pi/192) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(3))))))/2
0.40392100487189496264 = cos(25*pi/68) = sqrt(8-sqrt(2)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17)))))/4
0.40524131400498987091 = cos(47*pi/128) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2))))))/2
0.40673664307580020775 = cos(11*pi/30) = (sqrt(15)+sqrt(3)-sqrt(10-2*sqrt(5)))/8
0.41270702980439473705 = cos(35*pi/96) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(3)))))/2
0.41642956009763718256 = cos(93*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.41865973753742808668 = cos(29*pi/80) = sqrt(4-sqrt(8-sqrt(2)-sqrt(10)+2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.42755509343028209432 = cos(23*pi/64) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))/2
0.43861623853852763765 = cos(91*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.44228869021900128200 = cos(17*pi/48) = sqrt(2-sqrt(2-sqrt(2-sqrt(3))))/2
0.44573835577653826740 = cos(6*pi/17) = (-1-sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/16
0.44961132965460660005 = cos(45*pi/128) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2))))))/2
0.45399049973954679156 = cos(7*pi/20) = (sqrt(2)-sqrt(10)+2*sqrt(5+sqrt(5)))/8
0.45690387563042067656 = cos(67*pi/192) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(3))))))/2
0.46053871095824002363 = cos(89*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.47139673682599764856 = cos(11*pi/32) = sqrt(2-sqrt(2-sqrt(2-sqrt(2))))/2
0.48218377207912274852 = cos(87*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.48576339371634005627 = cos(65*pi/192) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(3))))))/2
0.48660447856685628729 = cos(23*pi/68) = sqrt(8-sqrt(2)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17)))))/4
0.48862124149695494742 = cos(27*pi/80) = sqrt(4-sqrt(8-sqrt(2)+sqrt(10)-2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.49289819222978403687 = cos(43*pi/128) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2))))))/2
0.50353838372571755869 = cos(85*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.51410274419322172659 = cos(21*pi/64) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))/2
0.52249856471594886499 = cos(13*pi/40) = sqrt(8-sqrt(2)+sqrt(10)-2*sqrt(5+sqrt(5)))/4
0.52458968267846890622 = cos(83*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.52643216287735580024 = cos(11*pi/34) = sqrt(2)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/8
0.52806785065036799587 = cos(31*pi/96) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(3)))))/2
0.53499761988709721066 = cos(41*pi/128) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2))))))/2
0.54189158057475171615 = cos(61*pi/192) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(3))))))/2
0.54463903501502708222 = cos(19*pi/60) = (sqrt(10)-sqrt(2)-sqrt(6)+sqrt(30)-2*(1-sqrt(3))*(sqrt(5+sqrt(5))))/16
0.54532498842204642231 = cos(81*pi/256) = sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.55236497296050581076 = cos(16*pi/51) = (1+sqrt(17)-sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/16
0.55557023301960222474 = cos(5*pi/16) = sqrt(2-sqrt(2-sqrt(2)))/2
0.56513641442259188898 = cos(21*pi/68) = sqrt(8-sqrt(2)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17)))))/4
0.56573181078361319739 = cos(79*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.56910014587889823061 = cos(59*pi/192) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(3))))))/2
0.57580819141784530075 = cos(39*pi/128) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2))))))/2
0.58247769686780214920 = cos(29*pi/96) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(3)))))/2
0.58579785745643886033 = cos(77*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.58778525229247312917 = cos(3*pi/10) = (sqrt(10-2*sqrt(5)))/4
0.59569930449243334347 = cos(19*pi/64) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))/2
0.60263463637925638918 = cos(5*pi/17) = (1+sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/16
0.60551104140432551392 = cos(75*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.60876142900872063942 = cos(7*pi/24) = sqrt(2-sqrt(2-sqrt(3)))/2
0.61523159058062684548 = cos(37*pi/128) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2))))))/2
0.61909394930983398694 = cos(23*pi/80) = sqrt(4-sqrt(8+sqrt(2)-sqrt(10)-2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.62166057337007740804 = cos(55*pi/192) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(3))))))/2
0.62485948814238637708 = cos(73*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.62932039104983745271 = cos(17*pi/60) = (sqrt(2)+sqrt(6)+sqrt(10)+sqrt(30)+2*(1-sqrt(3))*(sqrt(5-sqrt(5))))/16
0.63439328416364549822 = cos(9*pi/32) = sqrt(2-sqrt(2-sqrt(2+sqrt(2))))/2
0.63884680565196131707 = cos(19*pi/68) = sqrt(8-sqrt(2)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17)))))/4
0.64383154288979146507 = cos(71*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.64695615253485736540 = cos(53*pi/192) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(3))))))/2
0.64944804833018365573 = cos(11*pi/40) = sqrt(8-sqrt(2)-sqrt(10)+2*sqrt(5-sqrt(5)))/4
0.65061830020424211372 = cos(14*pi/51) = (1-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/32 + sqrt(6)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16
0.65317284295377676408 = cos(35*pi/128) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2))))))/2
0.65934581510006886843 = cos(13*pi/48) = sqrt(2-sqrt(2-sqrt(2+sqrt(3))))/2
0.66241577759017176111 = cos(69*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.66913060635885821383 = cos(4*pi/15) = (1-sqrt(5)+sqrt(30+6*sqrt(5)))/8
0.67155895484701840063 = cos(17*pi/64) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))/2
0.67369564364655721171 = cos(9*pi/34) = sqrt(2)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/8
0.67880074553294174139 = cos(21*pi/80) = sqrt(4-sqrt(8-sqrt(2)-sqrt(10)-2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.68060099779545305059 = cos(67*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.68359230202287128051 = cos(25*pi/96) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(3)))))/2
0.68954054473706692462 = cos(33*pi/128) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2))))))/2
0.69544263500961165112 = cos(49*pi/192) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(3))))))/2
0.69613394596292660828 = cos(13*pi/51) = (-1-sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/16
0.69837624940897285355 = cos(65*pi/256) = sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.70710678118654752440 = cos(pi/4) = sqrt(2)/2
0.71573082528381865413 = cos(63*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.71858161777969805720 = cos(47*pi/192) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(3))))))/2
0.72424708295146692094 = cos(31*pi/128) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2))))))/2
0.72986407269783565735 = cos(23*pi/96) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(3)))))/2
0.73265427167241283462 = cos(61*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.73432250943568553564 = cos(19*pi/80) = sqrt(4+sqrt(8-sqrt(2)-sqrt(10)-2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.73900891722065911592 = cos(4*pi/17) = (-1+sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/16
0.74095112535495909118 = cos(15*pi/64) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))/2
0.74314482547739423501 = cos(7*pi/30) = (sqrt(15)-sqrt(3)+sqrt(10+2*sqrt(5)))/8
0.74913639452345932547 = cos(59*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.75183980747897739641 = cos(11*pi/48) = sqrt(2+sqrt(2-sqrt(2+sqrt(3))))/2
0.75720884650648454758 = cos(29*pi/128) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2))))))/2
0.76040596560003093817 = cos(9*pi/40) = sqrt(8+sqrt(2)+sqrt(10)-2*sqrt(5-sqrt(5)))/4
0.76252720390638809637 = cos(43*pi/192) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(3))))))/2
0.76516726562245892589 = cos(57*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.76933397098287890812 = cos(15*pi/68) = sqrt(8+sqrt(2)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17)))))/4
0.77301045336273696081 = cos(7*pi/32) = sqrt(2+sqrt(2-sqrt(2+sqrt(2))))/2
0.77714596145697087998 = cos(13*pi/60) = (sqrt(6)-sqrt(2)-sqrt(10)+sqrt(30)+2*(1+sqrt(3))*(sqrt(5-sqrt(5))))/16
0.77908057452567043192 = cos(11*pi/51) = (-1+sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/32 + sqrt(6)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/16
0.78073722857209447830 = cos(55*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.78328674922865036540 = cos(41*pi/192) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(3))))))/2
0.78531693088074492747 = cos(17*pi/80) = sqrt(4+sqrt(8+sqrt(2)-sqrt(10)-2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.78834642762660626201 = cos(27*pi/128) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2))))))/2
0.79335334029123516458 = cos(5*pi/24) = sqrt(2+sqrt(2-sqrt(3)))/2
0.79583690460888353626 = cos(53*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.79801722728023950333 = cos(7*pi/34) = sqrt(2)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/8
0.80320753148064490981 = cos(13*pi/64) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))/2
0.80901699437494742410 = cos(pi/5) = (sqrt(5)+1)/4
0.81045719825259479173 = cos(51*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.81284668459161521658 = cos(19*pi/96) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(3)))))/2
0.81619691235622169087 = cos(10*pi/51) = (1-sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/32 + sqrt(6)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/16
0.81758481315158369650 = cos(25*pi/128) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2))))))/2
0.82226821898977510784 = cos(37*pi/192) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(3))))))/2
0.82458930278502526447 = cos(49*pi/256) = sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.82499747459830231554 = cos(13*pi/68) = sqrt(8+sqrt(2)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17)))))/4
0.83146961230254523708 = cos(3*pi/16) = sqrt(2+sqrt(2-sqrt(2)))/2
0.83822470555483804319 = cos(47*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.83867056794542402964 = cos(11*pi/60) = (sqrt(6)-sqrt(2)+sqrt(10)-sqrt(30)+2*(1+sqrt(3))*(sqrt(5+sqrt(5))))/16
0.84044840109443802102 = cos(35*pi/192) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(3))))))/2
0.84485356524970707326 = cos(23*pi/128) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2))))))/2
0.84920218152657888765 = cos(17*pi/96) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(3)))))/2
0.85021713572961415213 = cos(3*pi/17) = (1+sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/16
0.85135519310526514226 = cos(45*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.85264016435409222152 = cos(7*pi/40) = sqrt(8+sqrt(2)-sqrt(10)+2*sqrt(5+sqrt(5)))/4
0.85772861000027206990 = cos(11*pi/64) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))/2
0.86397285612158673792 = cos(43*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.86602540378443864676 = cos(pi/6) = sqrt(3)/2
0.87008699110871141865 = cos(21*pi/128) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2))))))/2
0.87249600707279711453 = cos(13*pi/80) = sqrt(4+sqrt(8-sqrt(2)+sqrt(10)-2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.87362239064636953713 = cos(11*pi/68) = sqrt(8+sqrt(2)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17)))))/4
0.87409034162675885155 = cos(31*pi/192) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(3))))))/2
0.87607009419540660710 = cos(41*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.88101219428578450601 = cos(8*pi/51) = (1+sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/16
0.88192126434835502971 = cos(5*pi/32) = sqrt(2+sqrt(2-sqrt(2-sqrt(2))))/2
0.88763962040285394776 = cos(39*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.88951607542185603527 = cos(29*pi/192) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(3))))))/2
0.89100652418836786236 = cos(3*pi/20) = (sqrt(10)-sqrt(2)+2*sqrt(5+sqrt(5)))/8
0.89322430119551532034 = cos(19*pi/128) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2))))))/2
0.89516329135506232207 = cos(5*pi/34) = sqrt(2)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/8
0.89687274153268830389 = cos(7*pi/48) = sqrt(2+sqrt(2-sqrt(2-sqrt(3))))/2
0.89867446569395384304 = cos(37*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.90398929312344333159 = cos(9*pi/64) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))/2
0.90814317382508129926 = cos(11*pi/80) = sqrt(4+sqrt(8-sqrt(2)-sqrt(10)+2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.90846527181952368611 = cos(7*pi/51) = (-1+sqrt(17)+sqrt(34-2*sqrt(17))-2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/32 + sqrt(6)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/16
0.90916798309052237656 = cos(35*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.91086382492117581857 = cos(13*pi/96) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(3)))))/2
0.91354545764260089550 = cos(2*pi/15) = (1+sqrt(5)+sqrt(30-6*sqrt(5)))/8
0.91420975570353065464 = cos(17*pi/128) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2))))))/2
0.91479386848802097000 = cos(9*pi/68) = sqrt(8+sqrt(2)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17)))))/4
0.91749449644749130792 = cos(25*pi/192) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(3))))))/2
0.91911385169005774391 = cos(33*pi/256) = sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.92387953251128675613 = cos(pi/8) = sqrt(2+sqrt(2))/2
0.92850608047321556594 = cos(31*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.93001722368401211706 = cos(23*pi/192) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(3))))))/2
0.93247222940435580457 = cos(2*pi/17) = (-1+sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16
0.93299279883473888771 = cos(15*pi/128) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2))))))/2
0.93358042649720174899 = cos(7*pi/60) = (sqrt(2)+sqrt(6)+sqrt(10)+sqrt(30)-2*(1-sqrt(3))*(sqrt(5-sqrt(5))))/16
0.93590592675732570029 = cos(11*pi/96) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(3)))))/2
0.93733901191257492320 = cos(29*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.93819133592248413445 = cos(9*pi/80) = sqrt(4+sqrt(8+sqrt(2)+sqrt(10)-2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.94154406518302077841 = cos(7*pi/64) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))/2
0.94560732538052132573 = cos(27*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.94693012949510566426 = cos(5*pi/48) = sqrt(2+sqrt(2+sqrt(2-sqrt(3))))/2
0.94816064759096585893 = cos(7*pi/68) = sqrt(8+sqrt(2)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17)))))/4
0.94952818059303666720 = cos(13*pi/128) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2))))))/2
0.95105651629515357212 = cos(pi/10) = (sqrt(10+2*sqrt(5)))/4
0.95206267771392425710 = cos(19*pi/192) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(3))))))/2
0.95294200042715655583 = cos(5*pi/51) = (-1+sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/32 + sqrt(6)*sqrt(17-sqrt(17)-sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16
0.95330604035419383692 = cos(25*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.95694033573220886494 = cos(3*pi/32) = sqrt(2+sqrt(2+sqrt(2-sqrt(2))))/2
0.96043051941556581120 = cos(23*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.96156179768296194714 = cos(17*pi/192) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(3))))))/2
0.96182564317281907041 = cos(3*pi/34) = sqrt(2)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/8
0.96245523645364728763 = cos(7*pi/80) = sqrt(4+sqrt(8+sqrt(2)-sqrt(10)+2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.96377606579543986669 = cos(11*pi/128) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2))))))/2
0.96592582628906828675 = cos(pi/12) = sqrt(2+sqrt(3))/2
0.96697647104485210909 = cos(21*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.96979693603500947182 = cos(4*pi/51) = (1+sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/16
0.97003125319454399260 = cos(5*pi/64) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))/2
0.97236992039767660183 = cos(3*pi/40) = sqrt(8-sqrt(2)+sqrt(10)+2*sqrt(5+sqrt(5)))/4
0.97293995220556014547 = cos(19*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.97343805436069282581 = cos(5*pi/68) = sqrt(8+sqrt(2)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17)))))/4
0.97387697927733364815 = cos(7*pi/96) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(3)))))/2
0.97570213003852854446 = cos(9*pi/128) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2))))))/2
0.97746197494357186339 = cos(13*pi/192) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(3))))))/2
0.97814760073380563793 = cos(pi/15) = (sqrt(5)-1+sqrt(30+6*sqrt(5)))/8
0.97831737071962763311 = cos(17*pi/256) = sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.98078528040323044913 = cos(pi/16) = sqrt(2+sqrt(2+sqrt(2)))/2
0.98297309968390177828 = cos(pi/17) = (1-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/16
0.98310548743121632718 = cos(15*pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2+sqrt(2)))))))/2
0.98384600592707741609 = cos(11*pi/192) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(3))))))/2
0.98527764238894124477 = cos(7*pi/128) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2))))))/2
0.98664333208487900475 = cos(5*pi/96) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(3)))))/2
0.98730141815785838240 = cos(13*pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2-sqrt(2)))))))/2
0.98768834059513772619 = cos(pi/20) = (sqrt(2)+sqrt(10)+2*(sqrt(5-sqrt(5))))/8
0.98917650996478097345 = cos(3*pi/64) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))/2
0.99041043087520515835 = cos(3*pi/68) = sqrt(8+sqrt(2)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17)))))/4
0.99090263542778002511 = cos(11*pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2-sqrt(2)))))))/2
0.99144486137381041114 = cos(pi/24) = sqrt(2+sqrt(2+sqrt(3)))/2
0.99242050967193575826 = cos(2*pi/51) = (1+sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/16
0.99247953459870999816 = cos(5*pi/128) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2))))))/2
0.99306845695492629564 = cos(3*pi/80) = sqrt(4+sqrt(8-sqrt(2)+sqrt(10)+2*sqrt(5+sqrt(5))))/2/sqrt(2)
0.99344777901944439551 = cos(7*pi/192) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(3))))))/2
0.99390697000235604155 = cos(9*pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2+sqrt(2)))))))/2
0.99452189536827333692 = cos(pi/30) = (sqrt(15)+sqrt(3)+sqrt(10-2*sqrt(5)))/8
0.99518472667219688624 = cos(pi/32) = sqrt(2+sqrt(2+sqrt(2+sqrt(2))))/2
0.99573417629503452187 = cos(pi/34) = sqrt(2)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17))))/8
0.99631261218277801263 = cos(7*pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2+sqrt(2)))))))/2
0.99665523930918032493 = cos(5*pi/192) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(3))))))/2
0.99691733373312797620 = cos(pi/40) = sqrt(8+sqrt(2)+sqrt(10)+2*sqrt(5-sqrt(5)))/4
0.99729045667869021614 = cos(3*pi/128) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2))))))/2
0.99785892323860350674 = cos(pi/48) = sqrt(2+sqrt(2+sqrt(2+sqrt(3))))/2
0.99810332873704407816 = cos(pi/51) = (-1-sqrt(17)+sqrt(34+2*sqrt(17))+2*sqrt(17-3*sqrt(17)-sqrt(34+2*sqrt(17))+2*sqrt(34-2*sqrt(17))))/32 + sqrt(6)*sqrt(17+sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(17-3*sqrt(17)+sqrt(34+2*sqrt(17))-2*sqrt(34-2*sqrt(17))))/16
0.99811811290014920713 = cos(5*pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2-sqrt(2)))))))/2
0.99862953475457387378 = cos(pi/60) = (sqrt(2)-sqrt(6)-sqrt(10)+sqrt(30)+2*(1+sqrt(3))*(sqrt(5+sqrt(5))))/16
0.99879545620517239271 = cos(pi/64) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))/2
0.99893297480237244441 = cos(pi/68) = sqrt(8+sqrt(2)*sqrt(17-sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(34+2*sqrt(17)))))/4
0.99922903624072293474 = cos(pi/80) = sqrt(4+sqrt(8+sqrt(2)+sqrt(10)+2*sqrt(5-sqrt(5))))/2/sqrt(2)
0.99932238458834950090 = cos(3*pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2-sqrt(2)))))))/2
0.99946458747636564443 = cos(pi/96) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(3)))))/2
0.99969881869620422012 = cos(pi/128) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2))))))/2
0.99986613790956178286 = cos(pi/192) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(3))))))/2
0.99992470183914454092 = cos(pi/256) = sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2+sqrt(2)))))))/2
0.01227153828571992608 = cos(127*π/256) = √2−√2+√2+√2+√2+√2+√2/2
0.01636173162648678164 = cos(95*π/192) = √2−√2+√2+√2+√2+√3/2
0.02454122852291228803 = cos(63*π/128) = √2−√2+√2+√2+√2+√2/2
0.03079505855617035387 = cos(25*π/51) = (−1−√17−√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17)/32 + √6*√17+√17−√34+2*√17−2*√17−3*√17−√34+2*√17+2*√34−2*√17/16
0.03271908282177614206 = cos(47*π/96) = √2−√2+√2+√2+√3/2
0.03680722294135883232 = cos(125*π/256) = √2−√2+√2+√2+√2+√2−√2/2
0.03925981575906860902 = cos(39*π/80) = √4−√8+√2+√10+2*√5−√5/2/√2
0.04618345864573959195 = cos(33*π/68) = √8−√2*√17−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17/4
0.04906767432741801425 = cos(31*π/64) = √2−√2+√2+√2+√2/2
0.05233595624294383272 = cos(29*π/60) = (√10−√2−√6+√30+2*(1−√3)*(√5+√5))/16
0.06132073630220857778 = cos(123*π/256) = √2−√2+√2+√2+√2−√2−√2/2
0.06540312923014306682 = cos(23*π/48) = √2−√2+√2+√3/2
0.07356456359966742353 = cos(61*π/128) = √2−√2+√2+√2+√2−√2/2
0.07845909572784494503 = cos(19*π/40) = √8−√2−√10−2*√5−√5/4
0.08172107413366822375 = cos(91*π/192) = √2−√2+√2+√2+√2−√3/2
0.08579731234443989046 = cos(121*π/256) = √2−√2+√2+√2+√2−√2+√2/2
0.09226835946330199524 = cos(8*π/17) = (−1+√17+√34−2*√17−2*√17+3*√17−√34−2*√17−2*√34+2*√17)/16
0.09801714032956060199 = cos(15*π/32) = √2−√2+√2+√2/2
0.10452846326765347140 = cos(7*π/15) = (√30−6*√5−√5−1)/8
0.11022220729388305881 = cos(119*π/256) = √2−√2+√2+√2−√2−√2+√2/2
0.11428696496684639812 = cos(89*π/192) = √2−√2+√2+√2−√2−√3/2
0.11753739745783764411 = cos(37*π/80) = √4−√8−√2+√10+2*√5+√5/2/√2
0.12241067519921619850 = cos(59*π/128) = √2−√2+√2+√2−√2−√2/2
0.13052619222005159155 = cos(11*π/24) = √2−√2+√3/2
0.13458070850712618632 = cos(117*π/256) = √2−√2+√2+√2−√2−√2−√2/2
0.13815635495188219823 = cos(31*π/68) = √8−√2*√17+√17+√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17/4
0.14673047445536175166 = cos(29*π/64) = √2−√2+√2+√2−√2/2
0.15339165487868537265 = cos(23*π/51) = (−1+√17+√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17)/32 − √6*√17−√17+√34−2*√17−2*√17+3*√17+√34−2*√17+2*√34+2*√17/16
0.15643446504023086901 = cos(9*π/20) = (√2+√10−2*(√5−√5))/8
0.15885814333386144168 = cos(115*π/256) = √2−√2+√2+√2−√2+√2−√2/2
0.16289547339458873948 = cos(43*π/96) = √2−√2+√2+√2−√3/2
0.17096188876030122636 = cos(57*π/128) = √2−√2+√2+√2−√2+√2/2
0.17901686127663268204 = cos(85*π/192) = √2−√2+√2+√2−√2+√3/2
0.18303988795514095852 = cos(113*π/256) = √2−√2+√2+√2−√2+√2+√2/2
0.18374951781657033157 = cos(15*π/34) = √2*√17−√17−√34−2*√17−2*√17+3*√17−√34−2*√17−2*√34+2*√17/8
0.19509032201612826785 = cos(7*π/16) = √2−√2+√2/2
0.20711137619221854971 = cos(111*π/256) = √2−√2+√2−√2−√2+√2+√2/2
0.20791169081775933710 = cos(13*π/30) = (√3−√15+√10+2*√5)/8
0.21111155235896516592 = cos(83*π/192) = √2−√2+√2−√2−√2+√3/2
0.21393308320649743991 = cos(22*π/51) = (1−√17+√34−2*√17−2*√17+3*√17+√34−2*√17+2*√34+2*√17)/32 + √6*√17−√17−√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17/16
0.21910124015686979723 = cos(55*π/128) = √2−√2+√2−√2−√2+√2/2
0.22707626303437320759 = cos(41*π/96) = √2−√2+√2−√2−√3/2
0.22895054995013407691 = cos(29*π/68) = √8−√2*√17+√17+√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17/4
0.23105810828067111964 = cos(109*π/256) = √2−√2+√2−√2−√2+√2−√2/2
0.23344536385590541177 = cos(17*π/40) = √8+√2−√10−2*√5+√5/4
0.24298017990326388995 = cos(27*π/64) = √2−√2+√2−√2−√2/2
0.25486565960451457155 = cos(107*π/256) = √2−√2+√2−√2−√2−√2−√2/2
0.25881904510252076235 = cos(5*π/12) = √2−√3/2
0.26671275747489838633 = cos(53*π/128) = √2−√2+√2−√2−√2−√2/2
0.27144044986507425334 = cos(33*π/80) = √4−√8+√2−√10+2*√5+√5/2/√2
0.27366299007208286354 = cos(7*π/17) = (1+√17−√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17)/16
0.27458861818493234148 = cos(79*π/192) = √2−√2+√2−√2−√2−√3/2
0.27851968938505310521 = cos(105*π/256) = √2−√2+√2−√2−√2−√2+√2/2
0.29028467725446236764 = cos(13*π/32) = √2−√2+√2−√2/2
0.30200594931922806700 = cos(103*π/256) = √2−√2+√2−√2+√2−√2+√2/2
0.30590302009655346276 = cos(77*π/192) = √2−√2+√2−√2+√2−√3/2
0.30901699437494742410 = cos(2*π/5) = (√5−1)/4
0.31368174039889147666 = cos(51*π/128) = √2−√2+√2−√2+√2−√2/2
0.31779141958190162617 = cos(27*π/68) = √8−√2*√17+√17−√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17/4
0.32143946530316158070 = cos(19*π/48) = √2−√2+√2−√3/2
0.32531029216226293414 = cos(101*π/256) = √2−√2+√2−√2+√2−√2−√2/2
0.33235479947965966456 = cos(20*π/51) = (1−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17)/32 − √6*√17−√17−√34−2*√17−2*√17+3*√17−√34−2*√17−2*√34+2*√17/16
0.33688985339222005069 = cos(25*π/64) = √2−√2+√2−√2+√2/2
0.34611705707749297647 = cos(31*π/80) = √4−√8+√2+√10−2*√5−√5/2/√2
0.34841868024943456842 = cos(99*π/256) = √2−√2+√2−√2+√2+√2−√2/2
0.35225004792123350653 = cos(37*π/96) = √2−√2+√2−√2+√3/2
0.35836794954530027348 = cos(23*π/60) = (√2−√6+√10−√30+2*(1+√3)*(√5−√5))/16
0.35989503653498814878 = cos(49*π/128) = √2−√2+√2−√2+√2+√2/2
0.36124166618715294874 = cos(13*π/34) = √2*√17−√17+√34−2*√17−2*√17+3*√17+√34−2*√17+2*√34+2*√17/8
0.36751593659470356541 = cos(73*π/192) = √2−√2+√2−√2+√2+√3/2
0.37131719395183754341 = cos(97*π/256) = √2−√2+√2−√2+√2+√2+√2/2
0.38268343236508977173 = cos(3*π/8) = √2−√2/2
0.38978587329267936908 = cos(19*π/51) = (−1−√17−√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17)/32 + √6*√17+√17−√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17/16
0.39399204006104810860 = cos(95*π/256) = √2−√2−√2−√2+√2+√2+√2/2
0.39774847452701105205 = cos(71*π/192) = √2−√2−√2−√2+√2+√3/2
0.40392100487189496264 = cos(25*π/68) = √8−√2*√17−√17−√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17/4
0.40524131400498987091 = cos(47*π/128) = √2−√2−√2−√2+√2+√2/2
0.40673664307580020775 = cos(11*π/30) = (√15+√3−√10−2*√5)/8
0.41270702980439473705 = cos(35*π/96) = √2−√2−√2−√2+√3/2
0.41642956009763718256 = cos(93*π/256) = √2−√2−√2−√2+√2+√2−√2/2
0.41865973753742808668 = cos(29*π/80) = √4−√8−√2−√10+2*√5−√5/2/√2
0.42755509343028209432 = cos(23*π/64) = √2−√2−√2−√2+√2/2
0.43861623853852763765 = cos(91*π/256) = √2−√2−√2−√2+√2−√2−√2/2
0.44228869021900128200 = cos(17*π/48) = √2−√2−√2−√3/2
0.44573835577653826740 = cos(6*π/17) = (−1−√17+√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17)/16
0.44961132965460660005 = cos(45*π/128) = √2−√2−√2−√2+√2−√2/2
0.45399049973954679156 = cos(7*π/20) = (√2−√10+2*√5+√5)/8
0.45690387563042067656 = cos(67*π/192) = √2−√2−√2−√2+√2−√3/2
0.46053871095824002363 = cos(89*π/256) = √2−√2−√2−√2+√2−√2+√2/2
0.47139673682599764856 = cos(11*π/32) = √2−√2−√2−√2/2
0.48218377207912274852 = cos(87*π/256) = √2−√2−√2−√2−√2−√2+√2/2
0.48576339371634005627 = cos(65*π/192) = √2−√2−√2−√2−√2−√3/2
0.48660447856685628729 = cos(23*π/68) = √8−√2*√17+√17−√34+2*√17−2*√17−3*√17−√34+2*√17+2*√34−2*√17/4
0.48862124149695494742 = cos(27*π/80) = √4−√8−√2+√10−2*√5+√5/2/√2
0.49289819222978403687 = cos(43*π/128) = √2−√2−√2−√2−√2−√2/2
0.50353838372571755869 = cos(85*π/256) = √2−√2−√2−√2−√2−√2−√2/2
0.51410274419322172659 = cos(21*π/64) = √2−√2−√2−√2−√2/2
0.52249856471594886499 = cos(13*π/40) = √8−√2+√10−2*√5+√5/4
0.52458968267846890622 = cos(83*π/256) = √2−√2−√2−√2−√2+√2−√2/2
0.52643216287735580024 = cos(11*π/34) = √2*√17+√17−√34+2*√17−2*√17−3*√17−√34+2*√17+2*√34−2*√17/8
0.52806785065036799587 = cos(31*π/96) = √2−√2−√2−√2−√3/2
0.53499761988709721066 = cos(41*π/128) = √2−√2−√2−√2−√2+√2/2
0.54189158057475171615 = cos(61*π/192) = √2−√2−√2−√2−√2+√3/2
0.54463903501502708222 = cos(19*π/60) = (√10−√2−√6+√30−2*(1−√3)*(√5+√5))/16
0.54532498842204642231 = cos(81*π/256) = √2−√2−√2−√2−√2+√2+√2/2
0.55236497296050581076 = cos(16*π/51) = (1+√17−√34+2*√17−2*√17−3*√17−√34+2*√17+2*√34−2*√17)/32 + √6*√17+√17+√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17/16
0.55557023301960222474 = cos(5*π/16) = √2−√2−√2/2
0.56513641442259188898 = cos(21*π/68) = √8−√2*√17−√17+√34−2*√17−2*√17+3*√17+√34−2*√17+2*√34+2*√17/4
0.56573181078361319739 = cos(79*π/256) = √2−√2−√2+√2−√2+√2+√2/2
0.56910014587889823061 = cos(59*π/192) = √2−√2−√2+√2−√2+√3/2
0.57580819141784530075 = cos(39*π/128) = √2−√2−√2+√2−√2+√2/2
0.58247769686780214920 = cos(29*π/96) = √2−√2−√2+√2−√3/2
0.58579785745643886033 = cos(77*π/256) = √2−√2−√2+√2−√2+√2−√2/2
0.58778525229247312917 = cos(3*π/10) = (√10−2*√5)/4
0.59569930449243334347 = cos(19*π/64) = √2−√2−√2+√2−√2/2
0.60263463637925638918 = cos(5*π/17) = (1+√17+√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17)/16
0.60551104140432551392 = cos(75*π/256) = √2−√2−√2+√2−√2−√2−√2/2
0.60876142900872063942 = cos(7*π/24) = √2−√2−√3/2
0.61523159058062684548 = cos(37*π/128) = √2−√2−√2+√2−√2−√2/2
0.61909394930983398694 = cos(23*π/80) = √4−√8+√2−√10−2*√5+√5/2/√2
0.62166057337007740804 = cos(55*π/192) = √2−√2−√2+√2−√2−√3/2
0.62485948814238637708 = cos(73*π/256) = √2−√2−√2+√2−√2−√2+√2/2
0.62932039104983745271 = cos(17*π/60) = (√2+√6+√10+√30+2*(1−√3)*(√5−√5))/16
0.63439328416364549822 = cos(9*π/32) = √2−√2−√2+√2/2
0.63884680565196131707 = cos(19*π/68) = √8−√2*√17−√17−√34−2*√17−2*√17+3*√17−√34−2*√17−2*√34+2*√17/4
0.64383154288979146507 = cos(71*π/256) = √2−√2−√2+√2+√2−√2+√2/2
0.64695615253485736540 = cos(53*π/192) = √2−√2−√2+√2+√2−√3/2
0.64944804833018365573 = cos(11*π/40) = √8−√2−√10+2*√5−√5/4
0.65061830020424211372 = cos(14*π/51) = (1−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17)/32 + √6*√17−√17−√34−2*√17−2*√17+3*√17−√34−2*√17−2*√34+2*√17/16
0.65317284295377676408 = cos(35*π/128) = √2−√2−√2+√2+√2−√2/2
0.65934581510006886843 = cos(13*π/48) = √2−√2−√2+√3/2
0.66241577759017176111 = cos(69*π/256) = √2−√2−√2+√2+√2−√2−√2/2
0.66913060635885821383 = cos(4*π/15) = (1−√5+√30+6*√5)/8
0.67155895484701840063 = cos(17*π/64) = √2−√2−√2+√2+√2/2
0.67369564364655721171 = cos(9*π/34) = √2*√17−√17−√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17/8
0.67880074553294174139 = cos(21*π/80) = √4−√8−√2−√10−2*√5−√5/2/√2
0.68060099779545305059 = cos(67*π/256) = √2−√2−√2+√2+√2+√2−√2/2
0.68359230202287128051 = cos(25*π/96) = √2−√2−√2+√2+√3/2
0.68954054473706692462 = cos(33*π/128) = √2−√2−√2+√2+√2+√2/2
0.69544263500961165112 = cos(49*π/192) = √2−√2−√2+√2+√2+√3/2
0.69613394596292660828 = cos(13*π/51) = (−1−√17+√34+2*√17−2*√17−3*√17−√34+2*√17+2*√34−2*√17)/32 + √6*√17+√17+√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17/16
0.69837624940897285355 = cos(65*π/256) = √2−√2−√2+√2+√2+√2+√2/2
0.70710678118654752440 = cos(π/4) = √2/2
0.71573082528381865413 = cos(63*π/256) = √2+√2−√2+√2+√2+√2+√2/2
0.71858161777969805720 = cos(47*π/192) = √2+√2−√2+√2+√2+√3/2
0.72424708295146692094 = cos(31*π/128) = √2+√2−√2+√2+√2+√2/2
0.72986407269783565735 = cos(23*π/96) = √2+√2−√2+√2+√3/2
0.73265427167241283462 = cos(61*π/256) = √2+√2−√2+√2+√2+√2−√2/2
0.73432250943568553564 = cos(19*π/80) = √4+√8−√2−√10−2*√5−√5/2/√2
0.73900891722065911592 = cos(4*π/17) = (−1+√17−√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17)/16
0.74095112535495909118 = cos(15*π/64) = √2+√2−√2+√2+√2/2
0.74314482547739423501 = cos(7*π/30) = (√15−√3+√10+2*√5)/8
0.74913639452345932547 = cos(59*π/256) = √2+√2−√2+√2+√2−√2−√2/2
0.75183980747897739641 = cos(11*π/48) = √2+√2−√2+√3/2
0.75720884650648454758 = cos(29*π/128) = √2+√2−√2+√2+√2−√2/2
0.76040596560003093817 = cos(9*π/40) = √8+√2+√10−2*√5−√5/4
0.76252720390638809637 = cos(43*π/192) = √2+√2−√2+√2+√2−√3/2
0.76516726562245892589 = cos(57*π/256) = √2+√2−√2+√2+√2−√2+√2/2
0.76933397098287890812 = cos(15*π/68) = √8+√2*√17−√17−√34−2*√17−2*√17+3*√17−√34−2*√17−2*√34+2*√17/4
0.77301045336273696081 = cos(7*π/32) = √2+√2−√2+√2/2
0.77714596145697087998 = cos(13*π/60) = (√6−√2−√10+√30+2*(1+√3)*(√5−√5))/16
0.77908057452567043192 = cos(11*π/51) = (−1+√17+√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17)/32 + √6*√17−√17+√34−2*√17−2*√17+3*√17+√34−2*√17+2*√34+2*√17/16
0.78073722857209447830 = cos(55*π/256) = √2+√2−√2+√2−√2−√2+√2/2
0.78328674922865036540 = cos(41*π/192) = √2+√2−√2+√2−√2−√3/2
0.78531693088074492747 = cos(17*π/80) = √4+√8+√2−√10−2*√5+√5/2/√2
0.78834642762660626201 = cos(27*π/128) = √2+√2−√2+√2−√2−√2/2
0.79335334029123516458 = cos(5*π/24) = √2+√2−√3/2
0.79583690460888353626 = cos(53*π/256) = √2+√2−√2+√2−√2−√2−√2/2
0.79801722728023950333 = cos(7*π/34) = √2*√17+√17−√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17/8
0.80320753148064490981 = cos(13*π/64) = √2+√2−√2+√2−√2/2
0.80901699437494742410 = cos(π/5) = (√5+1)/4
0.81045719825259479173 = cos(51*π/256) = √2+√2−√2+√2−√2+√2−√2/2
0.81284668459161521658 = cos(19*π/96) = √2+√2−√2+√2−√3/2
0.81619691235622169087 = cos(10*π/51) = (1−√17−√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17)/32 + √6*√17−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17/16
0.81758481315158369650 = cos(25*π/128) = √2+√2−√2+√2−√2+√2/2
0.82226821898977510784 = cos(37*π/192) = √2+√2−√2+√2−√2+√3/2
0.82458930278502526447 = cos(49*π/256) = √2+√2−√2+√2−√2+√2+√2/2
0.82499747459830231554 = cos(13*π/68) = √8+√2*√17−√17+√34−2*√17−2*√17+3*√17+√34−2*√17+2*√34+2*√17/4
0.83146961230254523708 = cos(3*π/16) = √2+√2−√2/2
0.83822470555483804319 = cos(47*π/256) = √2+√2−√2−√2−√2+√2+√2/2
0.83867056794542402964 = cos(11*π/60) = (√6−√2+√10−√30+2*(1+√3)*(√5+√5))/16
0.84044840109443802102 = cos(35*π/192) = √2+√2−√2−√2−√2+√3/2
0.84485356524970707326 = cos(23*π/128) = √2+√2−√2−√2−√2+√2/2
0.84920218152657888765 = cos(17*π/96) = √2+√2−√2−√2−√3/2
0.85021713572961415213 = cos(3*π/17) = (1+√17+√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17)/16
0.85135519310526514226 = cos(45*π/256) = √2+√2−√2−√2−√2+√2−√2/2
0.85264016435409222152 = cos(7*π/40) = √8+√2−√10+2*√5+√5/4
0.85772861000027206990 = cos(11*π/64) = √2+√2−√2−√2−√2/2
0.86397285612158673792 = cos(43*π/256) = √2+√2−√2−√2−√2−√2−√2/2
0.86602540378443864676 = cos(π/6) = √3/2
0.87008699110871141865 = cos(21*π/128) = √2+√2−√2−√2−√2−√2/2
0.87249600707279711453 = cos(13*π/80) = √4+√8−√2+√10−2*√5+√5/2/√2
0.87362239064636953713 = cos(11*π/68) = √8+√2*√17+√17−√34+2*√17−2*√17−3*√17−√34+2*√17+2*√34−2*√17/4
0.87409034162675885155 = cos(31*π/192) = √2+√2−√2−√2−√2−√3/2
0.87607009419540660710 = cos(41*π/256) = √2+√2−√2−√2−√2−√2+√2/2
0.88101219428578450601 = cos(8*π/51) = (1+√17+√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17)/32 + √6*√17+√17−√34+2*√17−2*√17−3*√17−√34+2*√17+2*√34−2*√17/16
0.88192126434835502971 = cos(5*π/32) = √2+√2−√2−√2/2
0.88763962040285394776 = cos(39*π/256) = √2+√2−√2−√2+√2−√2+√2/2
0.88951607542185603527 = cos(29*π/192) = √2+√2−√2−√2+√2−√3/2
0.89100652418836786236 = cos(3*π/20) = (√10−√2+2*√5+√5)/8
0.89322430119551532034 = cos(19*π/128) = √2+√2−√2−√2+√2−√2/2
0.89516329135506232207 = cos(5*π/34) = √2*√17+√17+√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17/8
0.89687274153268830389 = cos(7*π/48) = √2+√2−√2−√3/2
0.89867446569395384304 = cos(37*π/256) = √2+√2−√2−√2+√2−√2−√2/2
0.90398929312344333159 = cos(9*π/64) = √2+√2−√2−√2+√2/2
0.90814317382508129926 = cos(11*π/80) = √4+√8−√2−√10+2*√5−√5/2/√2
0.90846527181952368611 = cos(7*π/51) = (−1+√17+√34−2*√17−2*√17+3*√17−√34−2*√17−2*√34+2*√17)/32 + √6*√17−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17/16
0.90916798309052237656 = cos(35*π/256) = √2+√2−√2−√2+√2+√2−√2/2
0.91086382492117581857 = cos(13*π/96) = √2+√2−√2−√2+√3/2
0.91354545764260089550 = cos(2*π/15) = (1+√5+√30−6*√5)/8
0.91420975570353065464 = cos(17*π/128) = √2+√2−√2−√2+√2+√2/2
0.91479386848802097000 = cos(9*π/68) = √8+√2*√17−√17−√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17/4
0.91749449644749130792 = cos(25*π/192) = √2+√2−√2−√2+√2+√3/2
0.91911385169005774391 = cos(33*π/256) = √2+√2−√2−√2+√2+√2+√2/2
0.92387953251128675613 = cos(π/8) = √2+√2/2
0.92850608047321556594 = cos(31*π/256) = √2+√2+√2−√2+√2+√2+√2/2
0.93001722368401211706 = cos(23*π/192) = √2+√2+√2−√2+√2+√3/2
0.93247222940435580457 = cos(2*π/17) = (−1+√17+√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17)/16
0.93299279883473888771 = cos(15*π/128) = √2+√2+√2−√2+√2+√2/2
0.93358042649720174899 = cos(7*π/60) = (√2+√6+√10+√30−2*(1−√3)*(√5−√5))/16
0.93590592675732570029 = cos(11*π/96) = √2+√2+√2−√2+√3/2
0.93733901191257492320 = cos(29*π/256) = √2+√2+√2−√2+√2+√2−√2/2
0.93819133592248413445 = cos(9*π/80) = √4+√8+√2+√10−2*√5−√5/2/√2
0.94154406518302077841 = cos(7*π/64) = √2+√2+√2−√2+√2/2
0.94560732538052132573 = cos(27*π/256) = √2+√2+√2−√2+√2−√2−√2/2
0.94693012949510566426 = cos(5*π/48) = √2+√2+√2−√3/2
0.94816064759096585893 = cos(7*π/68) = √8+√2*√17+√17−√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17/4
0.94952818059303666720 = cos(13*π/128) = √2+√2+√2−√2+√2−√2/2
0.95105651629515357212 = cos(π/10) = (√10+2*√5)/4
0.95206267771392425710 = cos(19*π/192) = √2+√2+√2−√2+√2−√3/2
0.95294200042715655583 = cos(5*π/51) = (−1+√17−√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17)/32 + √6*√17−√17−√34−2*√17+2*√17+3*√17−√34−2*√17−2*√34+2*√17/16
0.95330604035419383692 = cos(25*π/256) = √2+√2+√2−√2+√2−√2+√2/2
0.95694033573220886494 = cos(3*π/32) = √2+√2+√2−√2/2
0.96043051941556581120 = cos(23*π/256) = √2+√2+√2−√2−√2−√2+√2/2
0.96156179768296194714 = cos(17*π/192) = √2+√2+√2−√2−√2−√3/2
0.96182564317281907041 = cos(3*π/34) = √2*√17+√17+√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17/8
0.96245523645364728763 = cos(7*π/80) = √4+√8+√2−√10+2*√5+√5/2/√2
0.96377606579543986669 = cos(11*π/128) = √2+√2+√2−√2−√2−√2/2
0.96592582628906828675 = cos(π/12) = √2+√3/2
0.96697647104485210909 = cos(21*π/256) = √2+√2+√2−√2−√2−√2−√2/2
0.96979693603500947182 = cos(4*π/51) = (1+√17−√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17)/32 + √6*√17+√17+√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17/16
0.97003125319454399260 = cos(5*π/64) = √2+√2+√2−√2−√2/2
0.97236992039767660183 = cos(3*π/40) = √8−√2+√10+2*√5+√5/4
0.97293995220556014547 = cos(19*π/256) = √2+√2+√2−√2−√2+√2−√2/2
0.97343805436069282581 = cos(5*π/68) = √8+√2*√17+√17+√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17/4
0.97387697927733364815 = cos(7*π/96) = √2+√2+√2−√2−√3/2
0.97570213003852854446 = cos(9*π/128) = √2+√2+√2−√2−√2+√2/2
0.97746197494357186339 = cos(13*π/192) = √2+√2+√2−√2−√2+√3/2
0.97814760073380563793 = cos(π/15) = (√5−1+√30+6*√5)/8
0.97831737071962763311 = cos(17*π/256) = √2+√2+√2−√2−√2+√2+√2/2
0.98078528040323044913 = cos(π/16) = √2+√2+√2/2
0.98297309968390177828 = cos(π/17) = (1−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17)/16
0.98310548743121632718 = cos(15*π/256) = √2+√2+√2+√2−√2+√2+√2/2
0.98384600592707741609 = cos(11*π/192) = √2+√2+√2+√2−√2+√3/2
0.98527764238894124477 = cos(7*π/128) = √2+√2+√2+√2−√2+√2/2
0.98664333208487900475 = cos(5*π/96) = √2+√2+√2+√2−√3/2
0.98730141815785838240 = cos(13*π/256) = √2+√2+√2+√2−√2+√2−√2/2
0.98768834059513772619 = cos(π/20) = (√2+√10+2*(√5−√5))/8
0.98917650996478097345 = cos(3*π/64) = √2+√2+√2+√2−√2/2
0.99041043087520515835 = cos(3*π/68) = √8+√2*√17+√17+√34+2*√17+2*√17−3*√17+√34+2*√17−2*√34−2*√17/4
0.99090263542778002511 = cos(11*π/256) = √2+√2+√2+√2−√2−√2−√2/2
0.99144486137381041114 = cos(π/24) = √2+√2+√3/2
0.99242050967193575826 = cos(2*π/51) = (1+√17+√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17)/32 + √6*√17+√17−√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17/16
0.99247953459870999816 = cos(5*π/128) = √2+√2+√2+√2−√2−√2/2
0.99306845695492629564 = cos(3*π/80) = √4+√8−√2+√10+2*√5+√5/2/√2
0.99344777901944439551 = cos(7*π/192) = √2+√2+√2+√2−√2−√3/2
0.99390697000235604155 = cos(9*π/256) = √2+√2+√2+√2−√2−√2+√2/2
0.99452189536827333692 = cos(π/30) = (√15+√3+√10−2*√5)/8
0.99518472667219688624 = cos(π/32) = √2+√2+√2+√2/2
0.99573417629503452187 = cos(π/34) = √2*√17−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17/8
0.99631261218277801263 = cos(7*π/256) = √2+√2+√2+√2+√2−√2+√2/2
0.99665523930918032493 = cos(5*π/192) = √2+√2+√2+√2+√2−√3/2
0.99691733373312797620 = cos(π/40) = √8+√2+√10+2*√5−√5/4
0.99729045667869021614 = cos(3*π/128) = √2+√2+√2+√2+√2−√2/2
0.99785892323860350674 = cos(π/48) = √2+√2+√2+√3/2
0.99810332873704407816 = cos(π/51) = (−1−√17+√34+2*√17+2*√17−3*√17−√34+2*√17+2*√34−2*√17)/32 + √6*√17+√17+√34+2*√17−2*√17−3*√17+√34+2*√17−2*√34−2*√17/16
0.99811811290014920713 = cos(5*π/256) = √2+√2+√2+√2+√2−√2−√2/2
0.99862953475457387378 = cos(π/60) = (√2−√6−√10+√30+2*(1+√3)*(√5+√5))/16
0.99879545620517239271 = cos(π/64) = √2+√2+√2+√2+√2/2
0.99893297480237244441 = cos(π/68) = √8+√2*√17−√17+√34−2*√17+2*√17+3*√17+√34−2*√17+2*√34+2*√17/4
0.99922903624072293474 = cos(π/80) = √4+√8+√2+√10+2*√5−√5/2/√2
0.99932238458834950090 = cos(3*π/256) = √2+√2+√2+√2+√2+√2−√2/2
0.99946458747636564443 = cos(π/96) = √2+√2+√2+√2+√3/2
0.99969881869620422012 = cos(π/128) = √2+√2+√2+√2+√2+√2/2
0.99986613790956178286 = cos(π/192) = √2+√2+√2+√2+√2+√3/2
0.99992470183914454092 = cos(π/256) = √2+√2+√2+√2+√2+√2+√2/2
The numerical values given in this table are rounded to 20 decimal places. They have been carefully calculated with bc to ensure that their numerical error is smaller than 5·10⁻²¹. Thus, the numerical values given here are far more accurate than those printed in the Character Tables, which are calculated by a Fortran floating point library and printed to 12 decimal places, with an error less than approximately 5·10⁻¹³.
In deriving that list, the famous identity cos(2φ)=2 cos2(φ)−1 is most helpful for cases with even denominators. For prime denominators, de Moivre’s formula (cos(2π/n) + i*sin(2π/n))n = 1 can be used (read: The n-th power of an n-th root of unity is one). Other cases are accessible by using the standard addition theorem cos(2π(n+m)/(n*m)) = cos(2π/n)*cos(2π/m) − sin(2π/n)*sin(2π/m). As usual, the worst part is the simplification of the resulting radical expression. Note that cosine values for angles with a given denominator differ only in the signs of the various terms and need not to be derived afresh.
This page was written by Gernot Katzer
See here for my Home Page
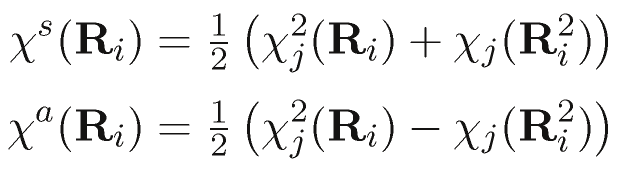 where Ri2 is the square of Ri (and therefore, in the general case, a distinct symmetry operation). With the additional information which symmetry operation is the square of a given symmetry operation, the antisymmetric product becomes available from the character table. However, this is almost moot as in all axial groups the antisymmetric product of an E with itself is always A2 (drop the 2 if it does not apply, and add a prime or a g if necessary), and it is only in the isometric groups that this result becomes interesting.
where Ri2 is the square of Ri (and therefore, in the general case, a distinct symmetry operation). With the additional information which symmetry operation is the square of a given symmetry operation, the antisymmetric product becomes available from the character table. However, this is almost moot as in all axial groups the antisymmetric product of an E with itself is always A2 (drop the 2 if it does not apply, and add a prime or a g if necessary), and it is only in the isometric groups that this result becomes interesting.